Pero
otros no terminales indirectamente también pueden ser
anulables.Los símbolos anulables son los no terminales de la gramática que se pueden anular, es decir, que pueden generar la palabra vacía.
Un no
terminal es anulable cuando existe una producción del tipo
Pero
otros no terminales indirectamente también pueden ser
anulables.
Por
ejemplo, si se tiene una producción del tipo
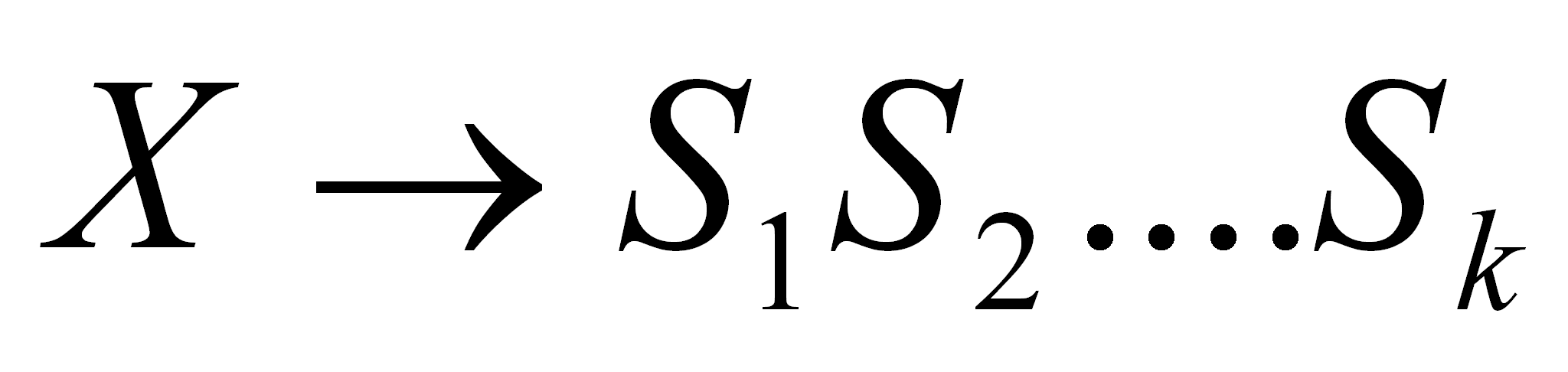y todos los símbolos
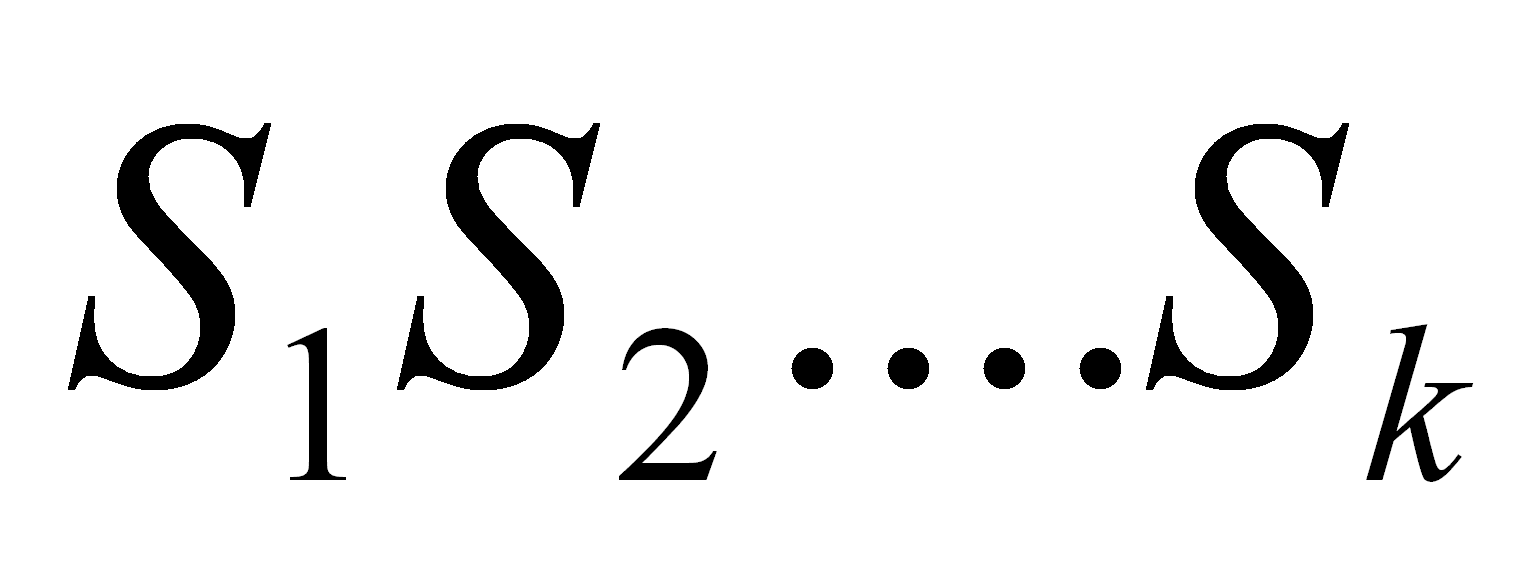son anulables entonces X también es anulable. El
procedimiento para el cálculo de los anulables se muestra en
el siguiente algoritmo (Algoritmo 1):
Entrada: Conjunto de no terminales (V)
Salida: La tabla Anulable registra si un símbolo es anulable o no.
1:
for all X
V
do
2: Anulable[X]:= false
3: end for
4: repeat
5:
for cada producción
do
6: if
not esAnulable
(X) and
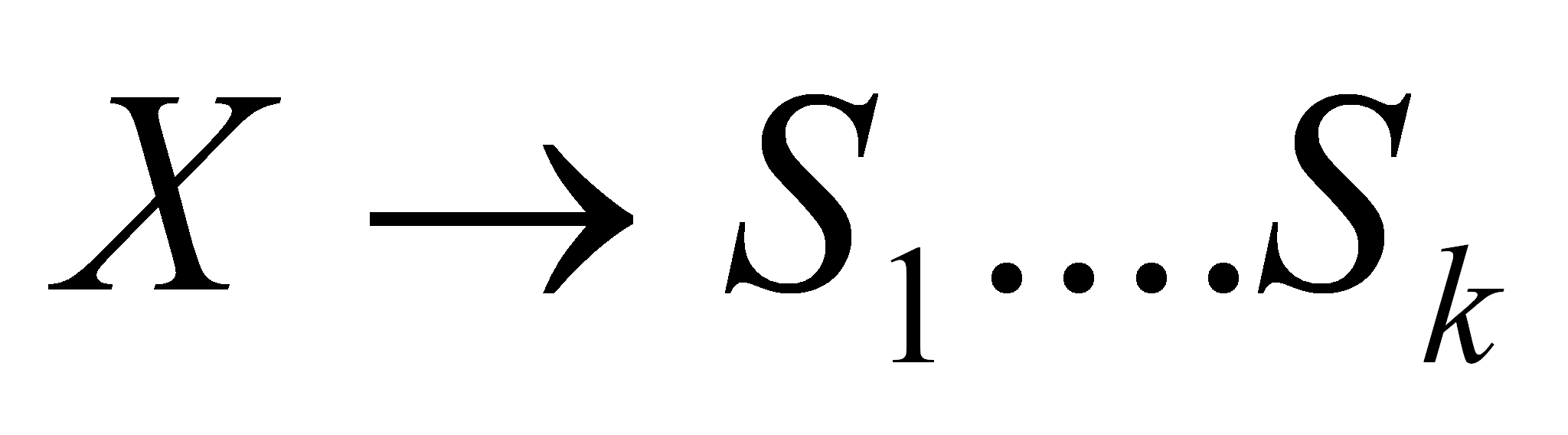son
todos anulables then
7: Anulable[X]:= true
8: end if
9: end for
10: until no hay más cambios
Algoritmo 1: Algoritmo de cálculo de la tabla de los símbolos anulables.
Por ejemplo, en la siguiente gramática:
S→ a |aAB
A→a |ε
B→A | bB
A sería un símbolo anulable, porque existe una producción directa donde A es nula.
(A→ ε). El otro símbolo anulable es B, porque aunque no exista una producción directa que lo anule, indirectamente se anula mediante la producción B→A.