Conjunto FIRST (Iniciales)
El
conjunto de iniciales (o FIRST) de una cadena
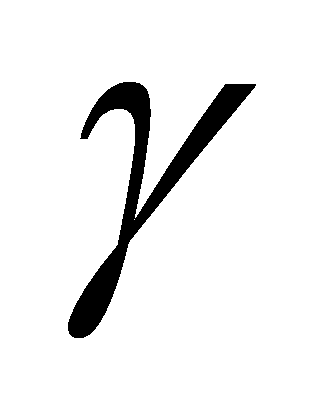 son el conjunto de terminales que pueden comenzar cualquier cadena
generada por la cadena
son el conjunto de terminales que pueden comenzar cualquier cadena
generada por la cadena
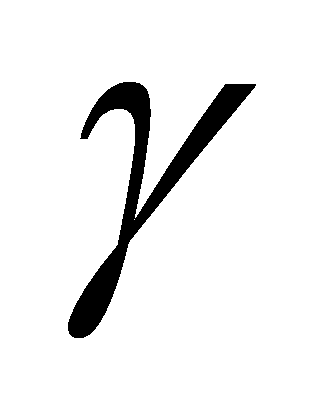 .
Donde .
Donde
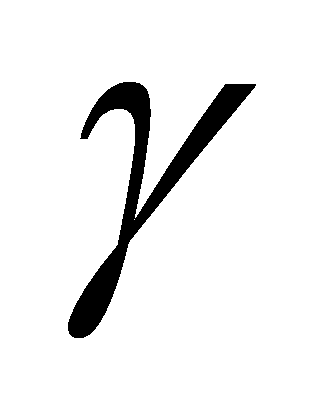 puede estar compuesta de terminales y no terminales.
puede estar compuesta de terminales y no terminales.
Para
calcular el FIRST de un símbolo X
se siguen las siguientes reglas:
1. Si X
es un terminal, entonces los iniciales de X
son {X}.
2. Si X
es un no terminal y X
→
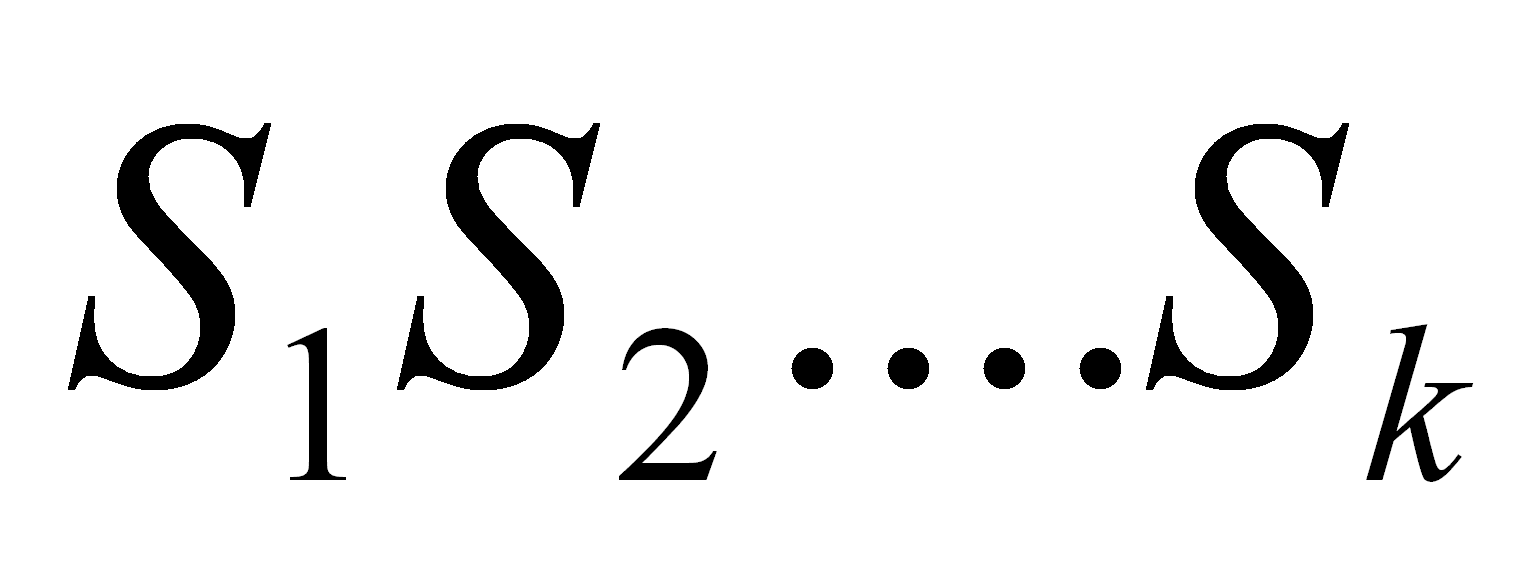 es
una producción, entonces agregar al FIRST de X,
el FIRST de es
una producción, entonces agregar al FIRST de X,
el FIRST de
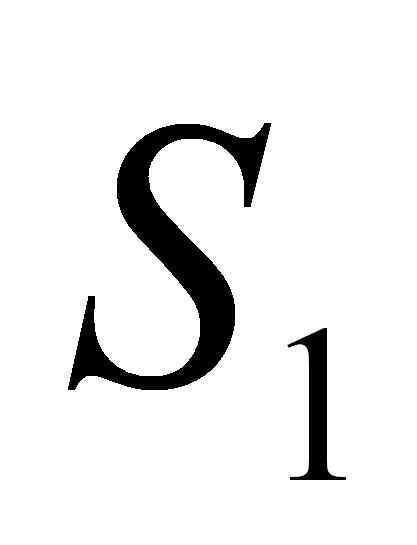 .
Además, si .
Además, si
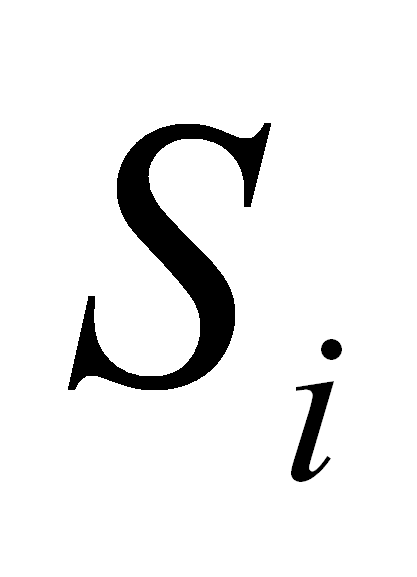 es
anulable añadir los iniciales de es
anulable añadir los iniciales de
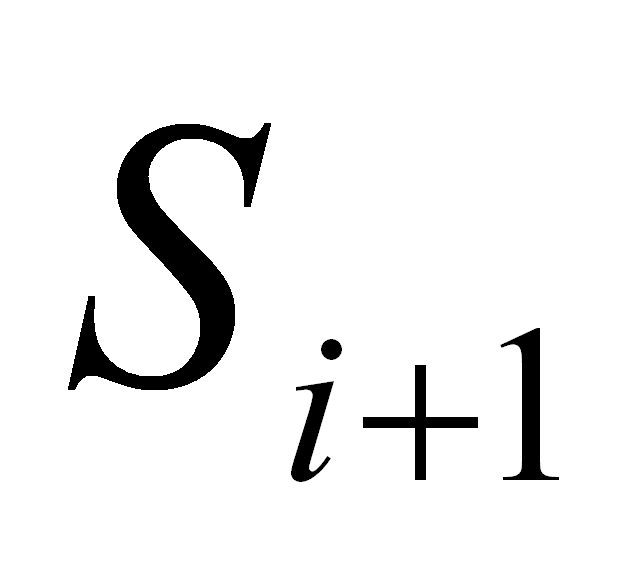 . .
Entrada:
Conjunto de terminales (T)
Salida:
la tabla FIRST, donde la clave es un símbolo y el valor es el
conjunto FIRST para dicho símbolo.
1:
for all t
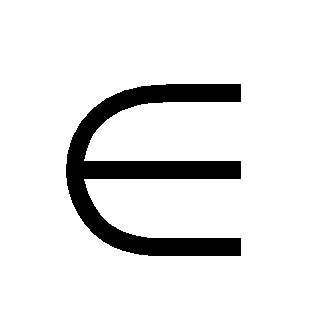 T do
T do
2:
FIRST[t]:=
{t}
3:
end for
4: for
cada producción
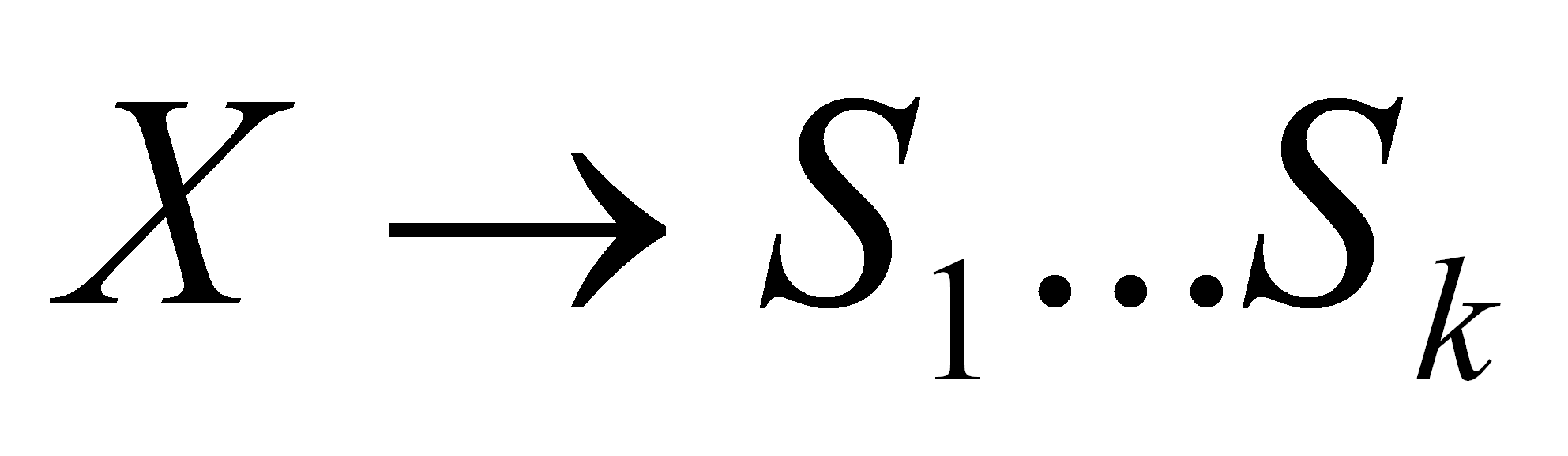 do do
5:
FIRST
[X]:=
FIRST
[X]
 FIRST
[ FIRST
[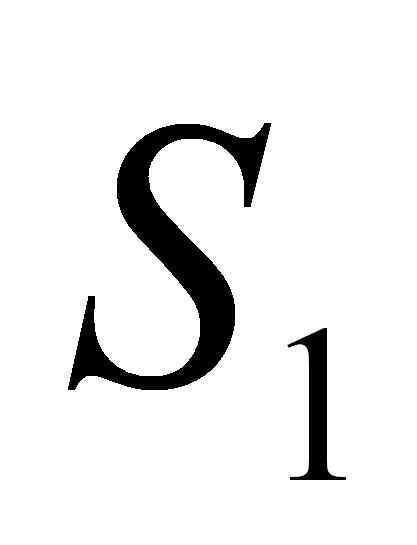 ] ]
6:
for i: = 2 to k do
7:
if esAnulable
(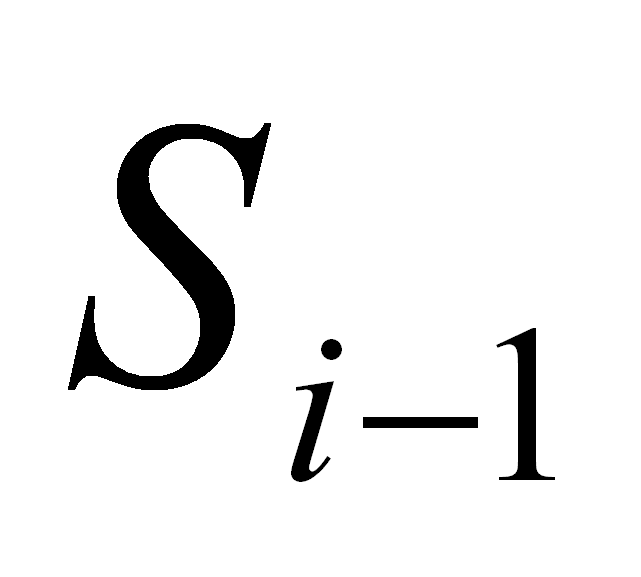 )
then )
then
8:
FIRST
[X]:=
FIRST
[X]  FIRST
[ FIRST
[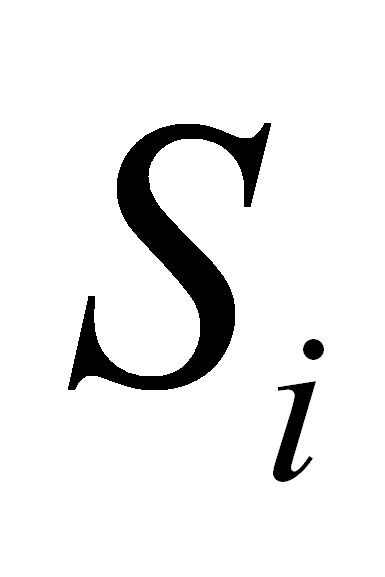 ] ]
9:
else
10:
break
11:
end if
12:
end for
13:
end for
Algoritmo
2: Algoritmo de cálculo
del conjunto FIRST.
Por
ejemplo, en la siguiente gramática:
Z
→ d | XYZ
Y
→ c | ε
X
→ a | Y
Su
conjunto FIRST sería:
X:{a,
c}
Y:{c}
Z:{a,
c, d}
El FIRST
de Y es
el más fácil de calcular, ya que aparte de la
producción nula sólo tiene otra producción y en
su parte derecha hay un terminal. Con lo cual en el FIRST de Y,
sólo está el terminal c.
En los iniciales de X
está el símbolo a,
este símbolo es debido directamente a la producción
X→a. El
símbolo c
viene dado por la producción X
→Y, ya que en el first de Y
estaba el símbolo c.
Con los iniciales de la Z
se hace igual. El primer inicial que hay que agregarle es la d,
que es debido a la producción Z→d.
Después
hay que agregarle el first de la X,
ya que es el primer símbolo de la producción X→XYZ.
Además, como el símbolo X
es anulable también hay que agregarle los de la Y.
Por último, como el símbolo Y
también es anulable, también hay que agregarle los del
símbolo Z,
que ya están añadidos.
|