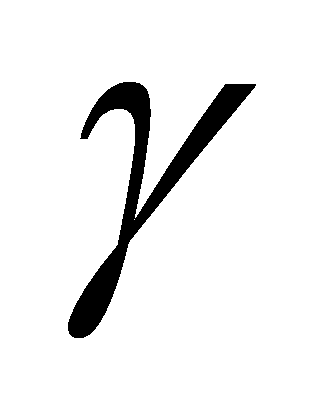 .
Donde
.
Donde
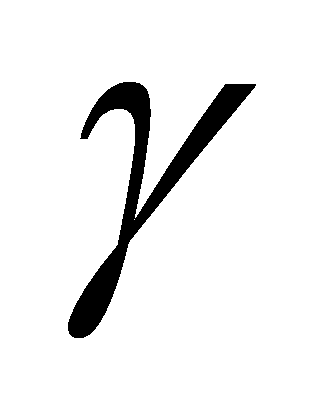 puede estar compuesta de terminales y no terminales.
puede estar compuesta de terminales y no terminales.El
conjunto de iniciales (o FIRST) de una cadena
![]() son el conjunto de terminales que pueden comenzar cualquier cadena
generada por la cadena
son el conjunto de terminales que pueden comenzar cualquier cadena
generada por la cadena
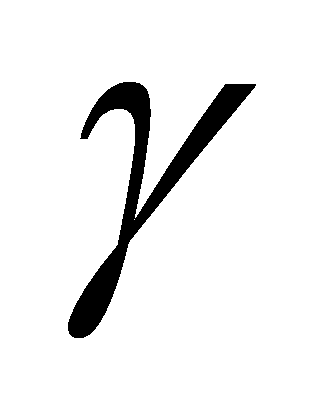 .
Donde
.
Donde
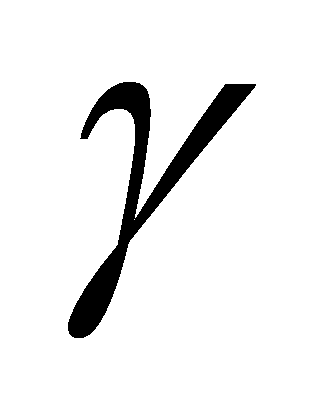 puede estar compuesta de terminales y no terminales.
puede estar compuesta de terminales y no terminales.
Para calcular el FIRST de un símbolo X se siguen las siguientes reglas:
1. Si X es un terminal, entonces los iniciales de X son {X}.
2. Si X
es un no terminal y X
→
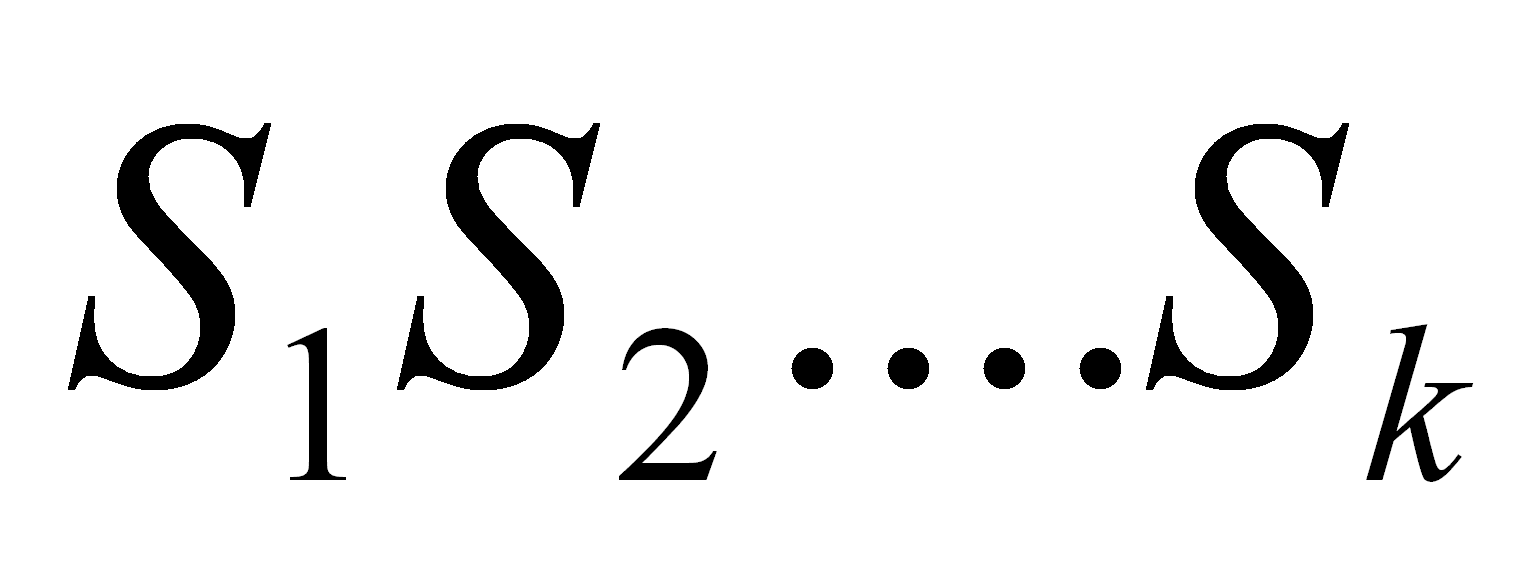 es
una producción, entonces agregar al FIRST de X,
el FIRST de
es
una producción, entonces agregar al FIRST de X,
el FIRST de
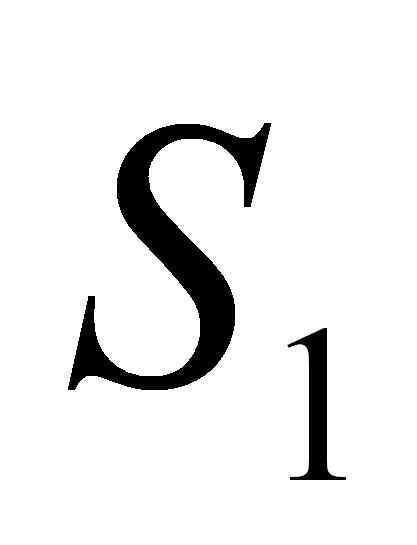 .
Además, si
.
Además, si
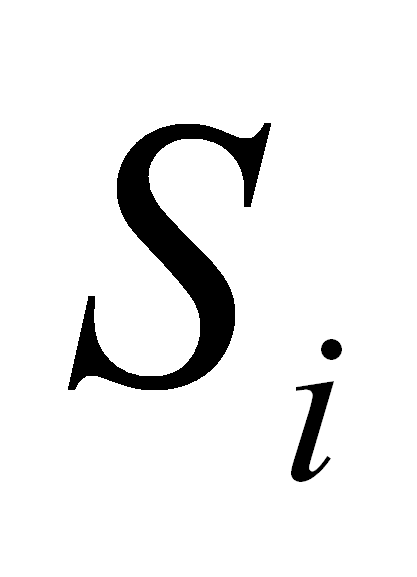 es
anulable añadir los iniciales de
es
anulable añadir los iniciales de
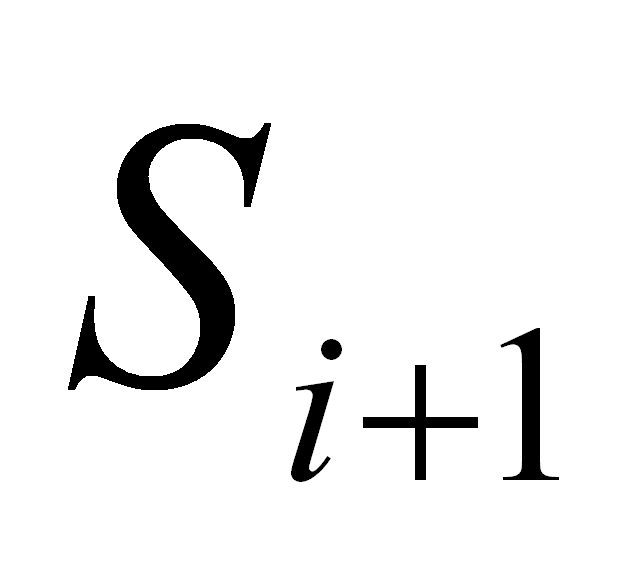 .
.
Entrada: Conjunto de terminales (T)
Salida: la tabla FIRST, donde la clave es un símbolo y el valor es el conjunto FIRST para dicho símbolo.
2: FIRST[t]:= {t}
3: end for
5:
FIRST
[X]:=
FIRST
[X]
 FIRST
[
FIRST
[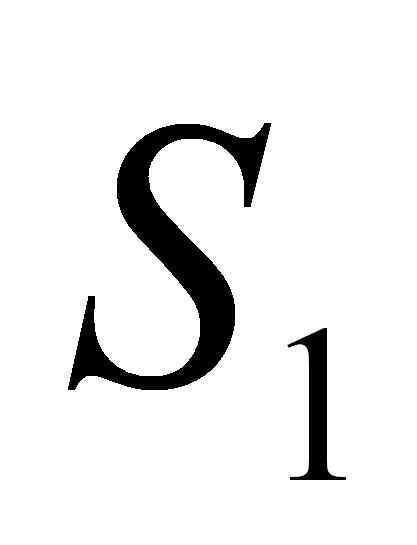 ]
]
6: for i: = 2 to k do
8:
FIRST
[X]:=
FIRST
[X]  FIRST
[
FIRST
[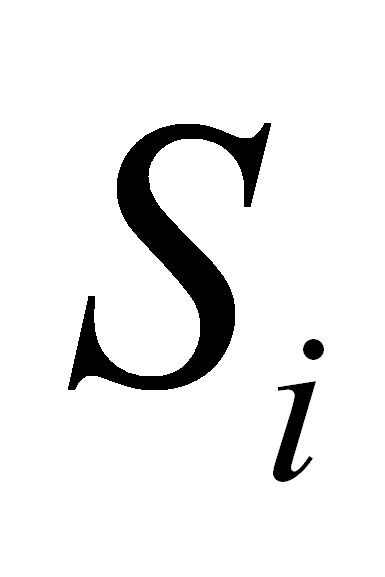 ]
]
9: else
10: break
11: end if
12: end for
13: end for
Algoritmo 2: Algoritmo de cálculo del conjunto FIRST.
Por ejemplo, en la siguiente gramática:
Z → d | XYZ
Y → c | ε
X → a | Y
Su conjunto FIRST sería:
X:{a, c}
Y:{c}
Z:{a, c, d}
El FIRST de Y es el más fácil de calcular, ya que aparte de la producción nula sólo tiene otra producción y en su parte derecha hay un terminal. Con lo cual en el FIRST de Y, sólo está el terminal c. En los iniciales de X está el símbolo a, este símbolo es debido directamente a la producción X→a. El símbolo c viene dado por la producción X →Y, ya que en el first de Y estaba el símbolo c. Con los iniciales de la Z se hace igual. El primer inicial que hay que agregarle es la d, que es debido a la producción Z→d.
Después hay que agregarle el first de la X, ya que es el primer símbolo de la producción X→XYZ. Además, como el símbolo X es anulable también hay que agregarle los de la Y. Por último, como el símbolo Y también es anulable, también hay que agregarle los del símbolo Z, que ya están añadidos.